|
QCDLoop
One-loop scalar Feynman integrals
|
#include <box.h>
Public Member Functions | |
| Box () | |
| The Constructor. | |
| ~Box () | |
| The Destructor. | |
| void | integral (vector< TOutput > &res, TScale const &mu2, vector< TMass > const &m, vector< TScale > const &p) |
| Computes the tadpole integral. More... | |
| void | B1 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,0,0,0;s12,s23;0,0,0,0) More... | |
| void | B2 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,0,0,p2;s12,s23;0,0,0,0) More... | |
| void | B3 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,pd2,0,pq2;s12,s23;0,0,0,0) More... | |
| void | B4 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,0,pt2,pq2;s12,s23;0,0,0,0) More... | |
| void | B5 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,pd2,pt2,pq2;s12,s23;0,0,0,0) More... | |
| void | B6 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,0,m2,m2;s12,s23;0,0,0,m2) More... | |
| void | B7 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,0,m2,pq2;s12,s23;0,0,0,m2) More... | |
| void | B8 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,0,pt2,pq2;s12,s23;0,0,0,m2) More... | |
| void | B9 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,p2,p3,m2;s12,s23;0,0,0,m2) More... | |
| void | B10 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,p2,p3,p4;s12,s23;0,0,0,m2) More... | |
| void | B11 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,m3,pt2,m4;s12,s23;0,0,m3,m4) More... | |
| void | B12 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,m3,pt2,pq2;s12,s23;0,0,m3,m4) More... | |
| void | B13 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(0,p2,p3,p4;s12,s23;0,0,m3,m4) More... | |
| void | B14 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(m2,m2,m4,m4;s12,s23;0,m2,0,m4) More... | |
| void | B15 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(m2,p2,p3,m4;s12,s23;0,m2,0,m4) More... | |
| void | B16 (vector< TOutput > &res, TMass const (&Y)[4][4], TScale const &mu2) const |
| Divergent box I(m2,p2,p3,m4;s12,s23;0,m2,m3,m4) More... | |
 Public Member Functions inherited from ql::Topology< TOutput, TMass, TScale > | |
| Topology (string name="None") | |
| Topology<TOutput, TMass>::Topology. More... | |
| Topology (const Topology &obj) | |
| Topology<TOutput, TMass>::Topology. More... | |
| virtual | ~Topology () |
| Topology<TOutput, TMass>::~Topology. | |
| string const & | getName () const |
| Get topology name. | |
| Public Member Functions inherited from ql::Tools< TOutput, TMass, TScale > | |
| Tools () | |
| The Constructor. | |
| ~Tools () | |
| The Destructor. | |
| bool | iszero (TMass const &psq) const |
| Check for zeros. More... | |
| TOutput | cLn (TOutput const &z, TScale const &isig) const |
| Log of complex argument with explicit sign for imag part. More... | |
| TOutput | cLn (TScale const &x, TScale const &isig) const |
| TOutput | fndd (int const &n, TOutput const &x, TScale const &iep) const |
| The fndd function. More... | |
| TOutput | Lnrat (TOutput const &x, TOutput const &y) const |
| Computes the ratio of logs. More... | |
| TOutput | Lnrat (TScale const &x, TScale const &y) const |
| TMass | ddilog (TMass const &x) const |
| Computes the dilog function for real argument. More... | |
| TOutput | denspence (TOutput const &z, TScale const &isig) const |
| Spence's function. More... | |
| TOutput | spencer (TOutput const &zrat1, TOutput const &zrat2, TScale const &ieps1, TScale const &ieps2) const |
| Spence's function for ratio arguments. More... | |
| TOutput | xspence (TOutput const (&z1)[2], TScale const (&im1)[2], TOutput const &z2, TScale const &im2) const |
| Difference of complex Spence's function. More... | |
| TOutput | cspence (TOutput const &z1, TScale const &im1, TOutput const &z2, TScale const &im2) const |
| Complex Spence's function. More... | |
| TOutput | Li2omrat (TScale const &x, TScale const &y) const |
| Expression for dilog(1-(x-i*ep)/(y-i*ep)). More... | |
| TOutput | Li2omrat (TOutput const &x, TOutput const &y, TScale const &ieps1=-1, TScale const &ieps2=-1) const |
| TOutput | Li2omx2 (TScale const &v, TScale const &w, TScale const &x, TScale const &y) const |
| Expression for dilog(1-(v-i*ep)*(w-i*ep)/(x-i*ep)/(y-i*ep)). More... | |
| TOutput | Li2omx2 (TOutput const &v, TOutput const &w, TOutput const &x, TOutput const &y, TScale const &ieps1=-1, TScale const &ieps2=-1) const |
| TOutput | cLi2omx2 (TOutput const &z1, TOutput const &z2, TScale const &ieps1=-1, TScale const &ieps2=-1) const |
| TOutput | Li2omx (TMass const &x1, TMass const &x2, TScale const &ieps1, TScale const &ieps2) const |
| Calculate Li[2](1-(x1+ieps1)*(x2+ieps2)) More... | |
| TOutput | cLi2omx3 (TOutput const &z1, TOutput const &z2, TOutput const &z3, TScale const &ieps1, TScale const &ieps2, TScale const &ieps3) const |
| Calculate Li[2](1-(z1+ieps1)*(z2+ieps2)*(z3+ieps3)) More... | |
| TOutput | L0 (TMass const &x, TMass const &y) const |
| TOutput | L1 (TMass const &x, TMass const &y) const |
| TOutput | R3int (TOutput const &p, TOutput const &s1, TOutput const &s2, TOutput const &t1) const |
| TOutput | R3int (TOutput const &p, TOutput const &s1, TOutput const &s2, TOutput const &t1, TOutput const &t2, TOutput const &t3, TOutput const &t4) const |
| TOutput | R2int (TOutput const &a, TOutput const &b, TOutput const &y0) const |
| TOutput | Rint (TOutput const &y, TOutput const &z, TScale const &ieps) const |
| void | R (TOutput &r, TOutput &d, TOutput const &q) const |
| Tools<TOutput, TMass, TScale>::R. More... | |
| TOutput | Zlogint (TOutput const &z, TScale const &ieps) const |
| Tools<TOutput, TMass, TScale>::qlZlogint. More... | |
| TOutput | ltspence (int const &i_in, TOutput const &z_in, TScale const &s) const |
| TOutput | li2series (TOutput const &z, TScale const &isig) const |
| TOutput | ltli2series (TOutput const &z1, TScale const &s) const |
| TOutput | eta2 (TOutput const &a, TOutput const &b) const |
| TOutput | eta3 (TOutput const &a, TOutput const &b, TOutput const &c) const |
| TOutput | eta5 (TOutput const &a, TOutput const &b, TOutput const &c, TOutput const &d, TOutput const &e) const |
| TOutput | xetatilde (TOutput const (&z1)[2], TScale const (&im1)[2], TOutput const &z2, TScale const &im2, TOutput const (&l1)[2]) const |
| TOutput | xeta (TOutput const (&z1)[2], TScale const (&im1)[2], TOutput const &z2, TScale const &im2, TScale const &im12, TOutput const (&l1)[2]) const |
| int | eta (TOutput const &z1, TScale const &s1, TOutput const &z2, TScale const &s2, TScale const &s12) const |
| int | etatilde (TOutput const &c1, TScale const &im1x, TOutput const &c2, TScale const &im2x) const |
| void | kfn (TOutput(&res)[3], TScale &ieps, TMass const &xpi, TMass const &xm, TMass const &xmp) const |
| The K-function. More... | |
| void | solveabc (TMass const &a, TMass const &b, TMass const &c, TOutput(&z)[2]) const |
| Solution of the quadratic equation. More... | |
| void | solveabcd (TOutput const &a, TOutput const &b, TOutput const &c, TOutput const &d, TOutput(&z)[2]) const |
| Solution of the quadratic equation passing the discriminant. More... | |
| void | solveabcd (TOutput const &a, TOutput const &b, TOutput const &c, TOutput(&z)[2]) const |
| void | ratgam (TOutput &ratp, TOutput &ratm, TScale &ieps, TMass const &p3sq, TMass const &m3sq, TMass const &m4sq) const |
| Ratio function. More... | |
| void | ratreal (TMass const &si, TMass const &ta, TMass &rat, TScale &ieps) const |
| Ratio function. More... | |
| Public Member Functions inherited from ql::LRUCache< size_t, vector< TOutput > > | |
| LRUCache (int const &size=1) | |
| LRUCache constructor. More... | |
| LRUCache (const LRUCache &obj) | |
| void | setCacheSize (int const &size) |
| Set the Cache size. | |
| int const & | getCacheSize () const |
| Get the Cache size. | |
| void | store (size_tconst &key, vector< TOutput >const &value) |
| Store the cached data. | |
| bool | get (size_tconst &key, vector< TOutput > &out) |
| Get the cached data. | |
Additional Inherited Members | |
| Public Types inherited from ql::LRUCache< size_t, vector< TOutput > > | |
| typedef std::pair< size_t, vector< TOutput > > | key_value_pair_t |
| typedef std::list< key_value_pair_t >::iterator | list_iterator_t |
| Protected Member Functions inherited from ql::Topology< TOutput, TMass, TScale > | |
| bool | checkCache (TScale const &, vector< TMass > const &, vector< TScale > const &) |
| < Check stored cached results More... | |
| void | storeCache (TScale const &, vector< TMass > const &, vector< TScale > const &) |
| Topology<TOutput, TMass>::storeCache. | |
| Protected Attributes inherited from ql::Topology< TOutput, TMass, TScale > | |
| string | _name |
| size_t | _key |
| TScale | _mu2 |
| vector< TMass > | _m |
| vector< TScale > | _p |
| vector< TOutput > | _val |
| ContainerHasher< TMass, TScale > * | _ch |
| Protected Attributes inherited from ql::Tools< TOutput, TMass, TScale > | |
| TScale | _pi |
| TScale | _pi2 |
| TScale | _pio3 |
| TScale | _pio6 |
| TScale | _pi2o3 |
| TScale | _pi2o6 |
| TScale | _pi2o12 |
| TScale | _zero |
| TScale | _half |
| TScale | _one |
| TScale | _two |
| TScale | _three |
| TScale | _four |
| TScale | _five |
| TScale | _six |
| TScale | _ten |
| TScale | _eps |
| TScale | _eps4 |
| TScale | _eps7 |
| TScale | _eps10 |
| TScale | _eps14 |
| TScale | _eps15 |
| TScale | _xloss |
| TScale | _neglig |
| TScale | _reps |
| TOutput | _2ipi |
| TOutput | _ipio2 |
| TOutput | _ipi |
| TOutput | _czero |
| TOutput | _chalf |
| TOutput | _cone |
| TOutput | _ctwo |
| TOutput | _cthree |
| TOutput | _cfour |
| TOutput | _ieps |
| TOutput | _ieps2 |
| TOutput | _ieps50 |
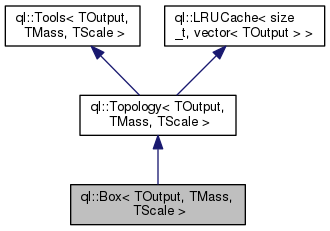
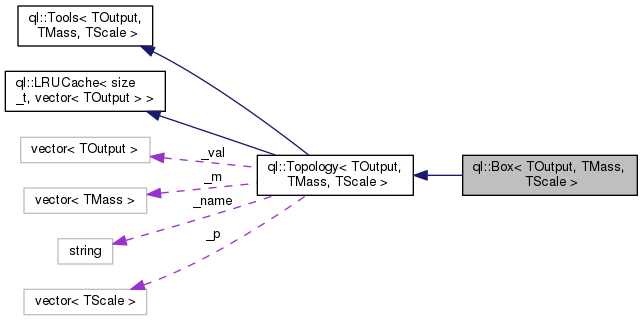
The Box integral.
Parses automatically the topology and computes the integral
| void ql::Box< TOutput, TMass, TScale >::B1 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,0,0,0;s12,s23;0,0,0,0)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,0,0,0;s_{12},s_{23};0,0,0,0) = \frac{\mu^{2\epsilon}}{s_{12}s_{23}}\left[ \frac{2}{\epsilon^2}\left( (-s_{12}-i\epsilon)^{-\epsilon} + (-s_{23}-i \epsilon)^{-\epsilon} \right) - \ln^2 \left( \frac{-s_{12}-i\epsilon}{-s_{23}-i\epsilon} \right) - \pi^2 \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Bern et al. [4].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B10 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,p2,p3,p4;s12,s23;0,0,0,m2)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,p_2^2,p_3^2,p_4^2;s_{12},s_{23};0,0,0,m^2) = \frac{1}{(s_{12}s_{23}-m^2 s_{12} - p_2^2 p_4^2 + m^2 p_2^2)} \\ \left[ \frac{1}{\epsilon} \ln \left( \frac{(m^2-p_4^2) p_2^2}{(m^2-s_{23})s_{12})} \right) + {\rm Li}_2 \left( 1 + \frac{(m^2-p_3^2)(m^2-s_{23})}{p_2^2 m^2} \right) - {\rm Li}_2 \left( 1 + \frac{(m^2-p_3^2)(m^2-p_4^2)}{s_{12} m^2} \right) \\ +2 {\rm Li}_2 \left( \right) - 2 {\rm Li}_2 \left( 1-\frac{p_2^2}{s_{12}} \right) + 2 {\rm Li}_2 \left( 1-\frac{p_2 (m^2-p_4^2)}{s_{12}(m^2-s_{23})} \right) \\ +2 \ln \left( \frac{\mu m}{m^2-s_{23}} \right) \ln \left( \frac{(m^2-p_4^2) p_2^2}{(m^2-s_{23}) s_{12}} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Ellis et al. [8].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B11 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,m3,pt2,m4;s12,s23;0,0,m3,m4)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,m_3^2,p_3^2,m_4^2;s_{12},s_{23};0,0,m_3^2,m_4^2) = \frac{1}{(m_3^2-s_{12})(m_4^2 - s_{23})} \\ \left[ \frac{1}{\epsilon^2} - \frac{1}{\epsilon} \ln \left( \frac{(m^2-s_{23})(m_3^2-s_{12})}{m_3 m_4 \mu^2} \right) + 2 \ln \left( \frac{m_3^2-s_{12}}{m_3 \mu} \right) \ln \left( \frac{m_4^2-s_{23}}{m_4 \mu} \right) \\ - \frac{\pi^2}{2} + \ln^2 \frac{m_3}{m_4} - \frac{1}{2} \ln^2 \left( \frac{\gamma^+_{34}}{\gamma^+_{34} - 1} \right) - \frac{1}{2} \ln \left( \frac{\gamma^-_{34}}{\gamma^-_{34} - 1} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Ellis et al. [8].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B12 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,m3,pt2,pq2;s12,s23;0,0,m3,m4)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,m_3^2,p_3^2,p_4^2;s_{12},s_{23};0,0,m_3^2,m_4^2) = \frac{1}{(s_{12}-m_3^2)(s_{23}-m_4^2)} \\ \left[ \frac{1}{2 \epsilon^2} - \frac{1}{\epsilon} \ln \left( \frac{(m_4^2-s_{23})(m_3^2-s_{12})}{(m_4-p_4^2) m_3 \mu} \right) + 2 \ln \left( \frac{m_4^2-s_{23}}{m_3 \mu} \right) \ln \left( \frac{m_3^2-s_{12}}{m_3 \mu} \right) \\ - \ln^2 \left( \frac{m_4^2-p_4^2}{m_3 \mu}\right) -\frac{\pi^2}{12} + \ln \left( \frac{m_4^2-p_4^2}{m_3^2-s_{12}} \right) \ln \left( \frac{m_4^2}{m_3^2} \right) - \frac{1}{2} \ln^2 \left( \frac{\gamma^+_{34}}{ \gamma^+_{34}-1 }\right) - \frac{1}{2} \ln^2 \left( \frac{\gamma^-_{34}}{\gamma^-_{34}-1} \right) \\ - 2 {\rm Li}_2 \left( 1 - \frac{(m_4^2-p_4^2)}{(m_4^2-s_{23})} \right) - {\rm Li}_2 \left( 1 - \frac{(m_4-p_4^2) \gamma^+_{43}}{(m_3^2-s_{12})(\gamma^+_{43}-1)} \right)- {\rm Li}_2 \left( 1 - \frac{(m_4-p_4^2) \gamma^-_{43}}{(m_3^2-s_{12})(\gamma^-_{43}-1)} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Ellis et al. [8].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B13 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,p2,p3,p4;s12,s23;0,0,m3,m4)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,p_2^2,p_3^2,p_4^2;s_{12},s_{23};0,0,m_3^2,m_4^2) = \frac{1}{\Delta} \left[ \frac{1}{\epsilon} \ln \left( \frac{(m_3^2-p_2^2)(m_4^2-p_4^2)}{(m_3^2-s_{12})(m_4^2-s_{23})} \right) \\ - 2 {\rm Li}_2 \left(1-\frac{(m_3^2-p_2^2)}{(m_3^2-s_{12})} \right) - {\rm Li}_2 \left( 1 - \frac{(m_3^2-p_2^2)\gamma^+_{34}}{(m_4^2-s_{23})(\gamma_{34}^+ - 1)} \right) - {\rm Li}_2 \left( 1 - \frac{(m_3^2-p_2^2)\gamma^-_{34}}{(m_4^2-s_{23})(\gamma_{34}^- - 1)} \right) \\ - 2 {\rm Li}_2 \left(1-\frac{(m_4^2-p_4^2)}{(m_4^2-s_{23})} \right) - {\rm Li}_2 \left( 1 - \frac{(m_4^2-p_4^2)\gamma^+_{43}}{(m_3^2-s_{12})(\gamma_{43}^+ - 1)} \right) - {\rm Li}_2 \left( 1 - \frac{(m_4^2-p_4^2)\gamma^-_{43}}{(m_2^2-s_{12})(\gamma_{43}^- - 1)} \right) \\ + 2 {\rm Li}_2 \left(1-\frac{(m_3^2-p_2^2)(m_4^2-p_4^2)}{(m_3^2-s_{12})(m_4^2-s_{23})} \right) + 2 \ln \left( \frac{m_3^2-s_{12}}{\mu^2} \right) \ln \left( \frac{m_4^2-s_{23}}{\mu^2} \right) \\ - \ln^2 \left( \frac{m_3^2-p_2^2}{\mu^2} \right) -ln^2 \left( \frac{m_4^2-p_4^2}{\mu^2} \right) + \ln \left( \frac{m_3^2-p_2^2}{m_4^2-s_{23}} \right) \ln \left( \frac{m_3^2}{\mu^2} \right) + \ln \left( \frac{m_4^2-p_4^2}{m_3^2 - s_{12}} \right) \ln \left( \frac{m_4^2}{\mu^2} \right) \\ -\frac{1}{2} \ln^2 \left( \frac{\gamma_{34}^+}{\gamma_{34}^+-1} \right) -\frac{1}{2} \ln^2 \left( \frac{\gamma_{34}^-}{\gamma_{34}^--1} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Ellis et al. [8].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B14 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(m2,m2,m4,m4;s12,s23;0,m2,0,m4)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(m_2^2,m_2^2,m_4^2,m_4^2;t,s;0,m_2^2,0,m_4^2) = \frac{-2}{m_2 m_4 t} \frac{x_s \ln x_s}{1-x_s^2} \left[ \frac{1}{\epsilon} + \ln \left( \frac{\mu^2}{-t} \right) \right],\, s-(m_2-m_4)^2 \neq 0 \\ = \frac{1}{m_2 m_4 t} \left[ \frac{1}{\epsilon} + \ln \left( \frac{\mu^2}{-t} \right) \right], s-(m_2-m_4)^2 = 0. \]
Implementation of the formulae from Beenakker et al. [1].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B15 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(m2,p2,p3,m4;s12,s23;0,m2,0,m4)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(m_2^2,p_2^2,p_3^2,m_4^2;t,s;0,m_2^2,0,m_4^2) = \\ \frac{x_s}{m_2 m_4 t (1-x_s^2)} \left\{ \ln x_s \left[ -\frac{1}{\epsilon} - \frac{1}{2} \ln x_s - \ln \left( \frac{\mu^2}{m_2 m_4} \right) - \ln \left( \frac{m_2^2-p_2^2}{-t} \right) - \ln \left( \frac{m_4^2-p_3^2}{-t} \right) \right] \\ - {\rm Li}_2 (1-x_s^2) + \frac{1}{2} ln^2 y + \sum_{\rho=\pm1} {\rm Li}_2 (1-x_s y^\rho) \right\} \]
Implementation of the formulae from Beenakker et al. [1].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B16 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(m2,p2,p3,m4;s12,s23;0,m2,m3,m4)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(m_2^2,p_2^2,p_3^2,m_4^2;t,s;0,m_2^2,m_3^2,m_4^2) = frac{x_s}{m_2 m_4 (t-m_3^2)(t-x_s^2)} \\ \left\{ - \frac{\ln x_s}{ \epsilon} - 2 \ln x_s \ln \left( \frac{m_3 \mu}{m_3^2-t} \right) + \ln^2 x_2 + \ln^2 x_3 - {\rm Li}_2 (1-x_s^2) \\ {\rm Li}_2 (1-x_s x_2 x_3) + {\rm Li}_2 \left( 1- \frac{x_s}{x_2 x_3} \right) + {\rm Li}_2 \left( 1- \frac{x_s x_2}{x_3} \right) + {\rm Li}_2 \left( 1- \frac{x_s x_3}{x_2} \right) \right\} \]
Implementation of the formulae from Beenakker et al. [1].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B2 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,0,0,p2;s12,s23;0,0,0,0)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,0,0,p_4^2;s_{12},s_{23};0,0,0,0) = \frac{\mu^{2\epsilon}}{s_{12}s_{23}}\left[ \frac{2}{\epsilon^2}\left( (-s_{12})^{-\epsilon} + (-s_{23})^{-\epsilon} -(-p_4^2)^{-\epsilon} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_4^2}{s_{12}} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_4^2}{s_{23}} \right) - \ln^2 \left( \frac{-s_{12}}{-s_{23}} \right) - \frac{\pi^2}{3} \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Bern et al. [4].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B3 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,pd2,0,pq2;s12,s23;0,0,0,0)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,p_2^2,0,p_4^2;s_{12},s_{23};0,0,0,0) = \frac{\mu^{2\epsilon}}{s_{12}s_{23}-p_4^2 p_2^2} \\ \left[ \frac{2}{\epsilon^2}\left( (-s_{12})^{-\epsilon} + (-s_{23})^{-\epsilon}-(-p_2^2)^{-\epsilon}-(-p_4^2)^{-\epsilon} \right) \\ - 2 {\rm Li}_2 \left( 1-\frac{p_2^2}{s_{12}} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_2^2}{s_{23}} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_4^2}{s_{12}} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_4^2}{s_{23}} \right) \\ + 2 {\rm Li}_2 \left( 1-\frac{p_4^2 p_2^2}{s_{23}s_{12}} \right) - \ln^2 \left( \frac{-s_{12}}{-s_{23}} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Bern et al. [4].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B4 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,0,pt2,pq2;s12,s23;0,0,0,0)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,0,p_3^2,p_4^2;s_{12},s_{23};0,0,0,0) = \frac{\mu^{2\epsilon}}{s_{12}s_{23}} \\ \left[ \frac{2}{\epsilon^2}\left( (-s_{12})^{-\epsilon} + (-s_{23})^{-\epsilon}-(-p_3^2)^{-\epsilon}-(-p_4^2)^{-\epsilon} \right) + \frac{1}{\epsilon^2} \left( (-p_3^2)^{-\epsilon}(-p_4)^{-\epsilon} \right) / (-s_{12})^{-\epsilon} \\ - 2 {\rm Li}_2 \left( 1-\frac{p_3^2}{s_{23}} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_4^2}{s_{23}} \right) - \ln^2 \left( \frac{-s_{12}}{-s_{23}} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Bern et al. [4].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B5 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,pd2,pt2,pq2;s12,s23;0,0,0,0)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,p_2^2,p_3^2,p_4^2;s_{12},s_{23};0,0,0,0) = \frac{\mu^{2\epsilon}}{s_{12}s_{23}-p_2^2 p_4^2} \\ \left[ \frac{2}{\epsilon^2}\left( (-s_{12})^{-\epsilon} + (-s_{23})^{-\epsilon}-(-p_2^2)^{-\epsilon}-(-p_3^2)^{-\epsilon} -(-p_4^2)^{-\epsilon} \right) \\ + \frac{1}{\epsilon^2} \left( (-p_2^2)^{-\epsilon}(-p_3)^{-\epsilon} \right) / (-s_{23})^{-\epsilon}+ \frac{1}{\epsilon^2} \left( (-p_3^2)^{-\epsilon}(-p_4)^{-\epsilon} \right) / (-s_{12})^{-\epsilon} \\ - 2 {\rm Li}_2 \left( 1-\frac{p_2^2}{s_{12}} \right) - 2 {\rm Li}_2 \left( 1-\frac{p_4^2}{s_{23}} \right) + 2 {\rm Li}_2 \left( 1-\frac{p_2^2 p_4^2}{s_{12} s_{23}} \right) - \ln^2 \left( \frac{-s_{12}}{-s_{23}} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Bern et al. [4].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B6 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,0,m2,m2;s12,s23;0,0,0,m2)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,0,m^2,m^2;s_{12},s_{23};0,0,0,m^2) = -\frac{1}{s_{12} (m^2-s_{23})} \left( \frac{\mu^2}{m^2} \right)^\epsilon \\ \left[ \frac{2}{\epsilon^2} - \frac{1}{\epsilon} \left( 2 \ln \left( \frac{m^2-s_{23}}{m^2} \right) + \ln \left( \frac{-s_{12}}{m^2} \right) \right) + 2 \ln \left( \frac{m^2-s_{23}}{m^2} \right) \ln \left( \frac{-s_{12}}{m^2} \right) - \frac{\pi^2}{2} \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Beenakker et al. [2].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B7 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,0,m2,pq2;s12,s23;0,0,0,m2)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,0,m^2,p_2^2;s_{12},s_{23};0,0,0,m^2) = \left( \frac{\mu^2}{m^2} \right)^\epsilon \frac{1}{s_{12} (s_{23}-m^2)} \\ \left[ \frac{3}{2 \epsilon^2} - \frac{1}{\epsilon} \left\{ 2 \ln \left( 1-\frac{s_{23}}{m^2} \right) + \ln \left( \frac{-s_{12}}{m^2} \right) - \ln \left( 1-\frac{p_4^2}{m^2} \right) \right\} \\ -2 {\rm Li}_2 \left( 1 - \frac{m^2-p_4^2}{m^2-s_{23}} \right) + 2 \ln \left( \frac{-s_{12}}{m^2} \right) \ln \left( 1-\frac{s_{23}}{m^2} \right) - \ln^2 \left( 1 - \frac{p_4^2}{m^2} \right) -\frac{5\pi^2}{12} \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Beenakker et al. [2].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B8 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,0,pt2,pq2;s12,s23;0,0,0,m2)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,0,p_3^2,p_4^2;s_{12},s_{23};0,0,0,m^2) = \frac{1}{s_{12} (s_{23}-m^2)} \left[ \frac{1}{\epsilon^2} - \frac{1}{\epsilon} \left[ \ln \frac{-s_{12}}{\mu^2} + \ln \frac{(m^2-s_{23}^2)}{(m^2-p_3^2)(m^2-p_4^2)} \right] \\ - 2 {\rm Li}_2 \left( 1 - \frac{m^2-p_3^2}{m^2-s_{23}} \right) - 2 {\rm Li}_2 \left( 1-\frac{m^2-p_4^2}{m^2-s_{23}} \right) - {\rm Li}_2 \left( 1 + \frac{(m^2-p_3^2)(m^2-p_4^2)}{s_{12} m^2} \right) \\ - \frac{\pi^2}{6} + \frac{1}{2} \ln^2 \left( \frac{-s_{12}}{\mu^2} \right) - \frac{1}{2} \ln^2 \left( \frac{-s_{12}}{m^2} \right) + 2 \ln \left( \frac{-s_{12}}{\mu^2} \right) \ln \left( \frac{m^2-s_{23}}{m^2} \right) \\ - \ln \left( \frac{m^2-p_3^2}{\mu^2} \right) \ln \left( \frac{m^2-p_3^2}{m^2} \right) - \ln \left( \frac{m^2-p_4^2}{\mu^2} \right) \ln \left( \frac{m^2-p_4^2}{m^2} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Beenakker et al. [2].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
| void ql::Box< TOutput, TMass, TScale >::B9 | ( | vector< TOutput > & | res, |
| TMass const (&) | Y[4][4], | ||
| TScale const & | mu2 | ||
| ) | const |
Divergent box I(0,p2,p3,m2;s12,s23;0,0,0,m2)
The integral is defined as:
\[ I_4^{D=4-2\epsilon}(0,p_2^2,p_3^2,m^2;s_{12},s_{23};0,0,0,m^2) = \frac{1}{s_{12} (s_{23}-m^2)} \left[ \frac{1}{2 \epsilon^2} - \frac{1}{\epsilon} \left( \frac{s_{12} (m^2-s_{23})}{p_2^2 \mu m} \right) \\ + {\rm Li}_2 \left(1+\frac{(m^2-p_3^2)(m^2-s_{23})}{m^2 p_2^2} \right) + 2 {\rm Li}_2 \left( 1-\frac{s_{12}}{p_2^2} \right) + \frac{\pi^2}{12} + \ln^2 \left( \frac{s_{12}(m^2-s_{23})}{p_2^2 \mu m} \right) \right] + \mathcal{O}(\epsilon) \]
Implementation of the formulae from Ellis et al. [8].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | the energy scale squared. |
|
virtual |
Computes the tadpole integral.
Computes the Box integral defined as:
\[ I_{4}^{D}(p_1^2,p_2^2,p_3^2,p_4^2;s_{12},s_{23};m_1^2,m_2^2,m_3^2,m_4^2)= \frac{\mu^{4-D}}{i \pi^{D/2} r_{\Gamma}} \int d^Dl \frac{1}{(l^2-m_1^2+i \epsilon)((l+q_1)^2-m_2^2+i \epsilon)((l+q_2)^2-m_3^2+i\epsilon)((l+q_4)^2-m_4^2+i\epsilon)} \]
where \( q_1=p_1, q_2=p_1+p_2, q_3=p_1+p_2+p_3\) and \(q_0=q_4=0\).
Implementation of the formulae of Denner et al. [6], 't Hooft and Veltman [9], Bern et al. [4].
| res | output object res[0,1,2] the coefficients in the Laurent series |
| mu2 | is the square of the scale mu |
| m | are the squares of the masses of the internal lines |
| p | are the four-momentum squared of the external lines |
Implements ql::Topology< TOutput, TMass, TScale >.
1.8.9.1
